アイアンooo ・ れんぞくxxx と今週来週の予定
2011年11月5日 TCG全般 コメント (3)
どうも、雑記の時間です。
前回、確率論についての記事を載せましたところ意外と評判が良かったため第二弾を書いてみました。しかし、実用性はあまりありませんよ。(^ω^)
最近”裏が出るまでコインを投げる”といった技を持つポケモンを良く見かけるような気がします。例えば、コマタナのアイアンヘッドやライチュウのアイアンテール、ドードリオのれんぞくつつきや最新のレシラムデッキではラッキーのれんぞくころがりなどが挙げられます。
そこで、質問です。これらのワザはどのぐらいのダメージを見込めるか直感で分かりますか??????
読んでくださる方の中には「そんなの当然分かる。」という方もいらっしゃれば「あれ?どうだろう?」と首をかしげる方もいらっしゃると思います。ちなみに、私は後者の方でした。
というわけで、求めてみました。基本的には皆さんに理解してもらいたいと思っていますので高校数学Aの範囲で説明したいと思いますが、申し訳ないことに今回は途中過程に数Bや数Ⅲのテクが入っています。前回同様、「数学なんてきらいじゃー! (><)」という方は過程をすっ飛ばして頂いてもかまいませんが、一応載せておきます。(誤りがあるかもしれませんので。)是非、変だと思ったところにはコメントで指摘してください。よろしくお願いします。m[_ _]m
また、ペイントで編集しましたので、小さくて少々見づらいかもしれませんが、そこは拡大して見てください。それと、画質が良くないのはご了承ください。
以下画像の解説
********************************
1枚目
コインは同様に確からしいとしてください。流体力学的に表がでやすいというような話とかは無しです。確率は難なく分かっていただけると思いますが、表のコインの枚数の期待値は
(表の枚数)×(その枚数だけ表になる確率)
の総和となりますので画像の下の方に書いてあるようになります。ただ、表の枚数の上限はありませんので、n番目の項の先は…となっています。
2枚目
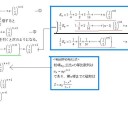
この期待値(E)をそのまま計算は出来ませんが、nを限りなく大きくすればn番目までの項の総和と求める期待値が同じ値になりますので、まずは、n番目までの項の総和(En)を求めます。そして、①式の両辺に1/2をかけて②式をつくり引きますが、その際に赤線の部分同士を引き算し、残りはそのままにしておくことがポイントです。すると、割と綺麗な形になります。次に等比数列の和の公式を緑線に適応し、最後に両辺に2をかければEnが出ます。
※書き忘れましたが、一行目の’これ’はEのことです。
3枚目
2枚目の解説に書きましたとおり、nを限りなく大きくします。すると、nの累乗の部分は限りなく0に近づきますので、その部分は0と考えます。うそだと思いましたら、1/2(0.5)を電卓なりで100万回かけてみたりして下さい。(笑)そのため、求めたい期待値は3枚目の画像に書いてあるようになります。
********************************
画像の解説おしまい
結論、
この手の技は1表出れば許容範囲なのかな。まあ、言われてみればそんな気もします。しかし、1ターン目に「アイアンヘッド使います。表18回でバトル場のEX
は気絶でベンチもいませんのでゲーム終了です。」とか一回やってみたいですね。(^^)
確率のお話おしまい
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
今度の休日は土浦へ行きます。
その次の週は土曜日はウジャさんの道場へ行きます。ネタでもいいかな?と思っていましたがウジャさんのほうから「ガチガチで来てください!!」とリクエストを頂きましたのでガチで臨もうと思います。しかし、ガチねぇ・・・・・・・何にしようかしら?(━_━)ゝウーム
ちなみに、他のブログにも書いてありますように興味をお持ちでしたら、連絡していただければ参加できると思います。ただ、皆さんは結構ガチらしいので(詳しくは知りませんが)、もし参加されるようであれば自信のあるデッキで参加することをオススメします。今回は盛り上がるだろうと思います。
日曜日は何もなければ通常通りジムチャレです。
前回、確率論についての記事を載せましたところ意外と評判が良かったため第二弾を書いてみました。しかし、実用性はあまりありませんよ。(^ω^)
最近”裏が出るまでコインを投げる”といった技を持つポケモンを良く見かけるような気がします。例えば、コマタナのアイアンヘッドやライチュウのアイアンテール、ドードリオのれんぞくつつきや最新のレシラムデッキではラッキーのれんぞくころがりなどが挙げられます。
そこで、質問です。これらのワザはどのぐらいのダメージを見込めるか直感で分かりますか??????
読んでくださる方の中には「そんなの当然分かる。」という方もいらっしゃれば「あれ?どうだろう?」と首をかしげる方もいらっしゃると思います。ちなみに、私は後者の方でした。
というわけで、求めてみました。基本的には皆さんに理解してもらいたいと思っていますので高校数学Aの範囲で説明したいと思いますが、申し訳ないことに今回は途中過程に数Bや数Ⅲのテクが入っています。前回同様、「数学なんてきらいじゃー! (><)」という方は過程をすっ飛ばして頂いてもかまいませんが、一応載せておきます。(誤りがあるかもしれませんので。)是非、変だと思ったところにはコメントで指摘してください。よろしくお願いします。m[_ _]m
また、ペイントで編集しましたので、小さくて少々見づらいかもしれませんが、そこは拡大して見てください。それと、画質が良くないのはご了承ください。
以下画像の解説
********************************
1枚目
コインは同様に確からしいとしてください。流体力学的に表がでやすいというような話とかは無しです。確率は難なく分かっていただけると思いますが、表のコインの枚数の期待値は
(表の枚数)×(その枚数だけ表になる確率)
の総和となりますので画像の下の方に書いてあるようになります。ただ、表の枚数の上限はありませんので、n番目の項の先は…となっています。
2枚目
この期待値(E)をそのまま計算は出来ませんが、nを限りなく大きくすればn番目までの項の総和と求める期待値が同じ値になりますので、まずは、n番目までの項の総和(En)を求めます。そして、①式の両辺に1/2をかけて②式をつくり引きますが、その際に赤線の部分同士を引き算し、残りはそのままにしておくことがポイントです。すると、割と綺麗な形になります。次に等比数列の和の公式を緑線に適応し、最後に両辺に2をかければEnが出ます。
※書き忘れましたが、一行目の’これ’はEのことです。
3枚目
2枚目の解説に書きましたとおり、nを限りなく大きくします。すると、nの累乗の部分は限りなく0に近づきますので、その部分は0と考えます。うそだと思いましたら、1/2(0.5)を電卓なりで100万回かけてみたりして下さい。(笑)そのため、求めたい期待値は3枚目の画像に書いてあるようになります。
********************************
画像の解説おしまい
結論、
この手の技は1表出れば許容範囲なのかな。まあ、言われてみればそんな気もします。しかし、1ターン目に「アイアンヘッド使います。表18回でバトル場のEX
は気絶でベンチもいませんのでゲーム終了です。」とか一回やってみたいですね。(^^)
確率のお話おしまい
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
今度の休日は土浦へ行きます。
その次の週は土曜日はウジャさんの道場へ行きます。ネタでもいいかな?と思っていましたがウジャさんのほうから「ガチガチで来てください!!」とリクエストを頂きましたのでガチで臨もうと思います。しかし、ガチねぇ・・・・・・・何にしようかしら?(━_━)ゝウーム
ちなみに、他のブログにも書いてありますように興味をお持ちでしたら、連絡していただければ参加できると思います。ただ、皆さんは結構ガチらしいので(詳しくは知りませんが)、もし参加されるようであれば自信のあるデッキで参加することをオススメします。今回は盛り上がるだろうと思います。
日曜日は何もなければ通常通りジムチャレです。



コメント
私は、表が出る度に、確率×1の長方形を積んでいき、面積の合計を期待値に見立ててみました。
1/2*1+1/4*1+1/8*1+1/16*1…→初項1/2、公比1/2の等比数列の和
ということで、結果は同じ1表ですね。
確かに、これは反復試行に近いので期待値を加算していくと求めたいものが出ますね。その発想は思いつかなかったです。
私も勉強させていただきました。
>ちずきごうさん
確率はあくまで目安にしかなりませんので、そういうこともよくあります。逆にぜんぜん表が出ないこともよくあります。私が投げる場合は裏のほうが多い気がしますが。(^^;)
以前、10表出されたときはビックリしました。(°0°)